考虑设备准备时间和生产平衡率的制药车间排产优化
文中提出了一种改进的多目标灰狼优化算法(IMOGWO)的柔性作业车间多目标排产方法,解决了制药车间生产工艺复杂、多品种小批量生产效率低及频繁清洗换型等问题。通过分析制药车间特点,建立了以完工时间、生产平衡率和设备利用率为优化目标的调度模型。采用变邻域搜索策略和逼近理想解排序法(TOPSIS)进行求解。试验结果表明:相比传统方法,IMOGWO算法能显著改善排产效果,包括最长完工时间缩短6天、生产平衡率提高14%、设备利用率提高11%,以及在制品临时库存方面的明显改善。
制药行业是一种典型的流程型制造业,与传统的离散型制造业相比,面临更多挑战和限制。药品生产过程中有复杂的操作步骤、高度精确的质量控制和严格的法规要求。同时,设备的清洗和换型时间、生产平衡率和设备利用率等因素也需要综合考虑。制药企业需要采用精细方法解决排产问题,合理安排生产计划,确保符合质量标准和法规要求,并充分发挥产能,实现高效生产。当前对制药车间排产问题的研究相对较少,需要提出有效的元启发式算法来解决多目标柔性车间排产问题,包括设备分配和生产顺序确定[1]。
灰狼优化算法(Grey Wolf Optimizer, GWO)是一种元启发式算法,灵感来源于灰狼捕食猎物的行为。GWO通过模拟灰狼群体的活动规律进行优化搜索[2]。该算法具有简单的搜索机制和快速收敛的特点,在解决复杂优化问题上表现出强大的性能[3-6]。为了改进GWO算法的全局探索能力和局部开发能力,成金海等[7]引入变邻域搜索策略,并将其应用于模糊车间调度问题的求解,研究结果表明:相比竞争算法,所提出的算法在解决该问题上显示出明显的优势。另一方面,时维国等[8]设计了改进的灰狼算法,用于解决柔性车间调度问题。唐红涛等[9]通过引入非线性函数和权重更新机制,将改进的灰狼算法应用于求解模糊车间调度问题。尽管许多学者通过引入不同的策略对灰狼优化算法进行了改进,但在对GWO的离散化和多目标优化的研究还相对较少[10-11]。此外,将GWO应用于最小化最长完工时间、最大化平衡率和设备利用率为优化目标的离散多目标非完全前沿流水车间调度问题的研究也很有限[12-14]。
文中提出了一种改进的多目标灰狼优化算法(IMOGWO)来解决制药车间排产优化问题。该算法考虑了设备准备时间和生产平衡率,并建立了一个数学模型以最小化最长完工时间、最大化生产平衡率和设备利用率为目标。通过引入灰狼优化算法和变邻域搜索策略,提高了算法的搜索能力和局部搜索能力。通过交换操作保留更优秀的个体,避免算法过早收敛。试验结果表明:相较于传统的人工经验排产,IMOGWO算法在提升产能效果方面显示出显著优势,验证了其在解决制药车间复杂排产问题上的有效性和可行性。
Part.01制药车间调度问题及模型
传统柔性作业车间调度问题涉及工序顺序和设备选择,而制药车间调度问题在此基础上增加了设备清洗换型约束和药品生产顺序约束。此问题要求在最小化清洗和换型次数的前提下,合理安排工序顺序和设备选择,同时考虑药品生产顺序和在制品有效期限制。因此,制药车间调度问题在排产计划中需要综合考虑设备清洗换型、药品生产顺序和在制品有效期等因素进行优化。
如图1所示,黑色方块代表设备清洗换型的时间,每台设备生产完一种产品后都需要进行清洗换型后才能够生产其他种类的药品。每种产品有多个批次,每个批次在一个工序生产完后即可进入下一个工序。同种药品不同批次在同一个工序不需要清洗换型。图1中,O1-1-2代表产品1在第1个工序上生产2批,其他编号依此类推。
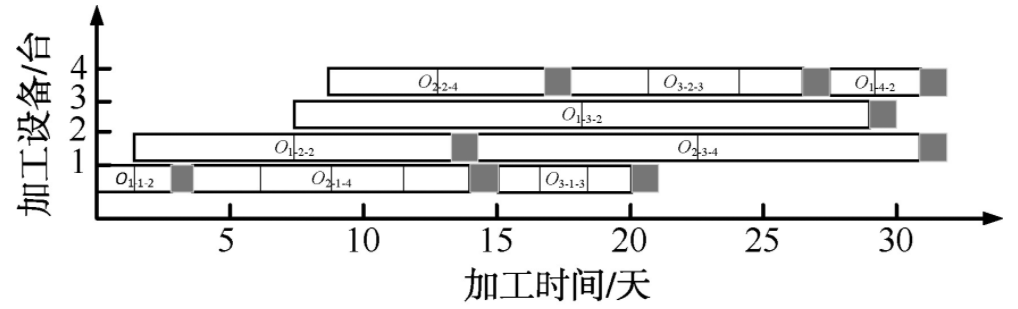
图 1 制药加工示意图
1.1模型假设和符号定义
IMOGWO算法模型的相关数学符号定义如表1所示。
表 1 符号表

相关假设如下:
(1) 每批药品的同一生产工序只能在一台设备上生产;
(2) 同一药品之间的生产工序有优先级约束,不同药品间的工序无优先级约束;
(3) 每道工序在不同设备上的加工时间是确定的;
(4) 每批产品在同一工序加工不可中断,直至该工序加工结束;
(5) 每个设备生产完一种药品后,必须清洗后才能生产其他种类的药品;
(6) 每台设备的清洗换型时间相同;
(7) 生产过程中设备均准时完成生产,不出现故障。
1.2目标函数
(1)所有工序总加工时间最短,即minTmax,用F1表示最小化最长生产周期为:
F1=minTmax=maxTn∀n(1)(2)各设备负荷率高,转化为所有设备总利用率高,用F2表示总的设备利用率为:
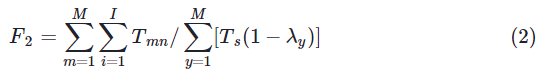
(3)同一工位组中所有工位负荷平衡,平衡率用F3表示,生产平衡率越高越好。
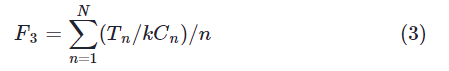
采用权重加合法得到调度总目标函数为:
F=max(ω1F1+ω2F2+ω3F3) (4)
式中:ω1,ω2,ω3——权重系数。
1.3约束条件
式(5)和式(6)规定了每批产品在每个工序只能分配给一个设备,允许每个设备分配0~I批产品。同时,式(7)确保每批产品只能在一台设备上生产。此外,式(8)确保每道工序加工不中断,直至工序结束。在同一工件的工序中,式(9)强调了高优先级工序的加工必须在所有高优先级工序完成后才能进行低优先级工序的加工。而式(10)表明每台设备只能同时进行一个工序的加工。最后,式(11)和(12)规定了每台设备在生产完一种产品后必须进行清洗,然后才能生产其他种类的药品,而在同一种药品的生产过程中则不需要清洗。
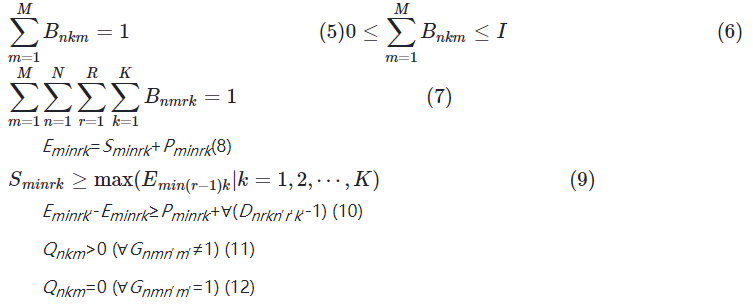
Part.02算法设计
灰狼优化算法是一种模拟灰狼捕食猎物行为的智能算法。该算法将灰狼群体分为4个层次,分别标记为α(个体最优解),β(优解),δ(次优解)狼及其他个体标记为ω狼。捕食过程主要分为包围、捕猎和攻击3个步骤。
步骤1 狼群对猎物进行包围,包围过程如式(13)~式(17)所示。
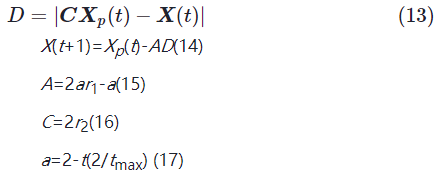
式中:D——猎物至灰狼间的距离;
t——当前迭代次数;
tmax——种群最大迭代次数;
A,C——协同系数向量;
Xp——猎物的位置向量;
X——灰狼的位置向量;
a——随着迭代过程从2~0线性递减;
r1,r2——[0,1]中的随机数向量。
步骤2 在包围完成后,由α,β,δ狼引导,其余狼群(ω狼)更新各自的位置。位置更新过程的数学表达式如下:
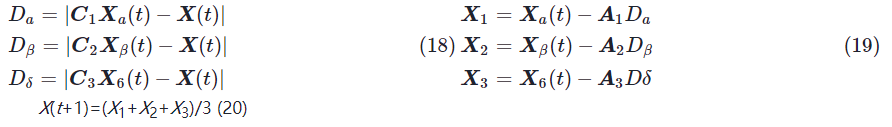
式(18)和式(19)计算灰狼个体与α,β和δ之间的距离,分析其对个体移动方向的影响。随后,采用式(20)确定个体在下一步猎物追逐中的移动方向。这一过程就是灰狼优化算法获得最优解的过程。
步骤3 该阶段狼群完成抓捕猎物,即得到最优解。
2.1种群初始化
在制药车间调度问题中,种群初始化是优化算法中的关键步骤,为了构建个体位置向量,将其分为两个部分:设备分配和生产排序。设备分配部分的构建可以借鉴[15]中的算法,通过优化搜索过程在搜索空间中寻找潜在解,并得到更优的设备分配结果,采用[16]中提出的方法来构建生产排序部分。首先,随机生成多个生产排序方案,不考虑顺序;然后,对每个排序方案进行评估,评估其与设备分配方案的组合效果;最终,通过比较评估结果,选择最优的一组作为初始调度解。这个种群初始化过程可以进行多次重复,直到得到满足要求的初始种群。
2.2种群更新机制
根据式(20),通过对适应度值X1,X2,X3进行加权平均,得到新的灰狼状态。然而,由于适应度值X1,X2,X3可能存在差异,对新状态的影响程度亦有所不同。仅采用权重平均分配无法精确反映不同层次狼群领导角色之间的差异,为了更有效地提升灰狼的适应性,文中引入动态加权的策略,以调整每只灰狼的适应度变化,即:
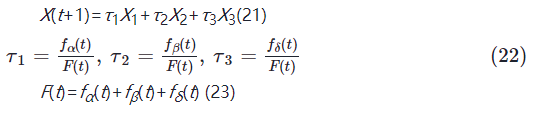
式中:F(t)——动态加权后的总的适应度值;
τ1,τ2,τ3——α,β,δ的权重系数;
fα(t),fβ(t),fδ(t)——α,β,δ个体适应度值。
2.3邻域局部搜索改进灰狼算法
为了避免陷入局部最优解,提高算法性能,使其能够更好地发现全局最优解。将局部搜索算法引入灰狼优化算法,并应用于3个个体α,β,δ。文中提出了3种邻域结构来支持局部搜索:
邻域结构N1在生产排序中,选择两个元素进行交换操作。这两个元素必须对应不同药品的工序,通过交换其位置,可以改变生产排序中的顺序,从而对整个生产过程进行优化。
邻域结构N2在生产排序中,选择两个元素,将后一个元素与第1个元素进行交换。这样可以改变元素的相对顺序,得到不同的解。
基于上述邻域结构,具体步骤如下:
步骤1 初始化解X,并设置阈值ψ>0。设定迭代次数上限ρ_max和终止迭代次数ρ。设置参数υ=1。
步骤2 若υ=1,则生成新解X′=N1(X)∪N3(X)。若υ=0,则生成新解X′=N2(X)∪N3(X)。
步骤3 若F(X′)-F(X)≤ψ成立,则更新解X=X′。否则,υ=|υ−1|υ=|υ-1|。
步骤4 增加迭代次数ρ。若满足ρ>ρ_max,则设置X′=X,转到步骤5。否则,转到步骤2。步骤5 算法终止。
2.4种群协同
为了有效平衡最长完工时间、生产平衡率和设备利用率这3个目标,引入了3个种群(PC,PE和PT)来处理位置更新,以减少因为集中于一个目标而导致的不平衡问题。在这3个种群中,PC主要致力于最小化最大完工时间;PE专注于最大化生产平衡率;PT则专注于最大化设备利用率。在每隔L次迭代时,对于PC,PE和PT这3个种群,进行个体的相互交换操作。首先,对PC种群按照最大完工时间的升序排列个体,选取前1/3的个体分别移动到PE和PT种群中;然后,对PE种群按生产平衡率的降序排列个体,取出前1/3的个体分别转移到PC和PT种群中;最后,对PT种群按设备利用率的降序排列个体,选取前1/3的个体分别移动到PC和PE种群中。通过这样的交换操作,每个种群都会增加1/3的个体,然后保留较优的个体,以维持种群的优势。这个过程旨在促进种群之间的信息交流和优良个体的传播,以提高整体优化效果。
2.5IMOGWO算法流程
将灰狼优化算法与种群更新机制、变邻域搜索策略和种群协同相结合,得到改进的多目标灰狼优化算法,算法流程如图2所示。
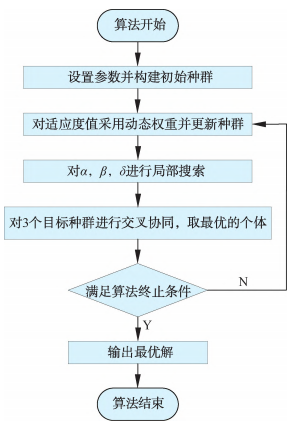
图 2 算法流程图
具体执行步骤如下:
步骤1 设置算法的种群个数和迭代次数,并根据2.3节中的方法初始化种群;
步骤2 采用动态权重方法来调整灰狼个体位置的更新,更新迭代参数;
步骤3 对α,β和δ执行局部搜索,然后根据适应度值的大小对其进行更新;
步骤4 根据第2.4节的种群协同机制进行种群间相互交换;步骤5 算法结束并输出最优解。
Part.03案例研究
3.1案例背景
目前,对于制药车间的生产排产算法研究较少,难以在文献中找到算例结果进行对比分析。为证明文中所提方法的可行性和有效性,以某药业公司口服制剂车间为研究对象,基于该车间的实际生产情况对模型进行初始化,并采用IMOGWO算法进行模型的求解与验证。该车间生产线属于典型的混流生产线,包括制粒、压片、包衣、填充、颗粒分装、粉碎筛分、瓶包及铝塑共8个生产工序,涉及22种设备和58种口服制剂产品。表2是该车间2023年12月的药品生产信息。
表 2 2023 年 12 月药品生产信息表
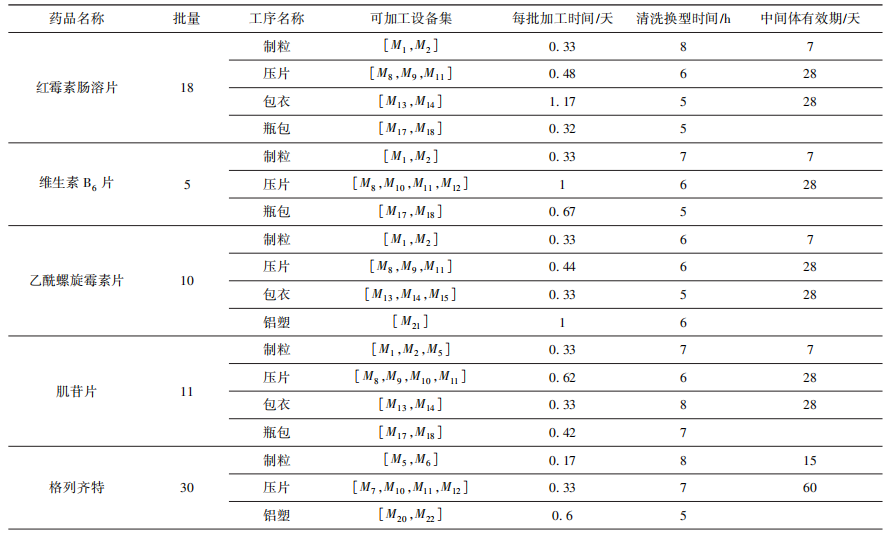
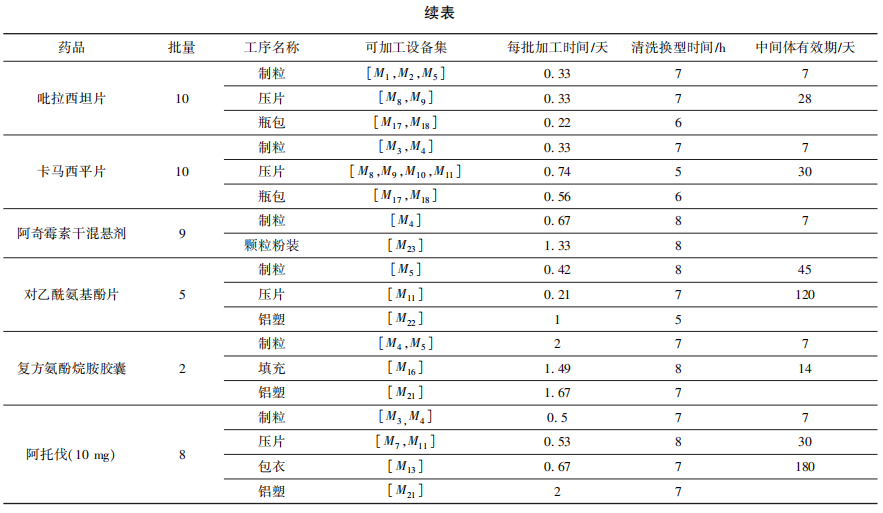
在2023年12月的生产中,总共有11种药品需要生产,其中,单个药品最大批量为30批,最小批量为2批。每种产品的工艺信息如表2所示,其中,每批加工时间根据设备产能计算得出,清洗换型时间包括设备清洁和检验时间,中间体有效期为制品临时储存的最长时间。
3.2模型求解
求解算法在MATLAB中编写,在得到的多组可行解中选取最优的结果。经过参数调整,初步确定初始种群规模N0=200,迭代次数G=200。鉴于IMOGWO算法的特征,若G值过大,将降低运行速度;若太小,则可能无法收敛。最终所选定的G值是经过多次试验得到的,试验结果显示,G值的设定对于帕累托解集的最佳结果具有关键性影响,其三维散点图如图3所示。
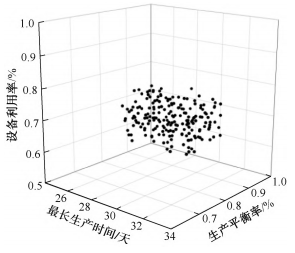
图 3 帕累托解集散点图
3.3排产方案排序
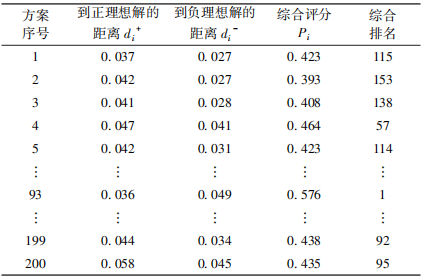
TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法是一种用于定量分析的方法。在文中通过TOPSIS方法对前面得到的Pareto解集进行评估,以获取最好的车间调度方案。根据制药车间实际情况,经分析讨论确定决策属性权重向量W= (0.4,0.2,0.4)。随后,对该权重向量进行加权标准化处理,得到正理想解U+= (0.048,6,0.020,7,0.044,2),负理想解U-= (0, 0, 0)。计算每个帕累托解到正理想解的距离(d+i)、到负理想解的距离(d-i)及相应的综合评分Pi。综合评分Pi通过d-i/(d-i+d+i)来定义,将计算结果整理在表3中,可评估帕累托解的相对性能,为决策提供更全面的信息。
表 3 IMOGWO 综合评价方案
3.4优化方案对比分析计
3.4.1 经验方案
目前,该车间主要根据排产者的经验来进行车间任务排产。2023年12月的经验排产方案如图4所示。排产者根据经验将11种药品分配在不同的可用设备上加工,由于人工排产的局限性,对于多目标排产不能很好地兼顾各个目标。根据该排产方案,可计算得到其最长完工时间为35天,生产平衡率为71%,设备利用率为63%,提升空间仍很大。
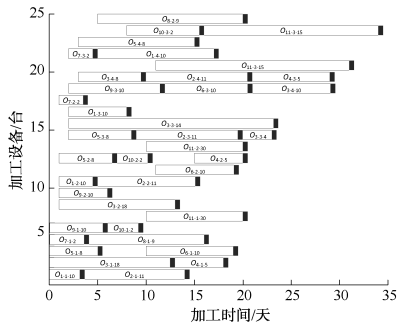
图 4 经验排产方案
3.4.2 IMOGWO排产方案
采用TOPSIS综合评价方法,对200个排产方案进行排序,发现方案93以总评分0.576居首,成为综合评价中的最佳选择。该方案最长完工时间为29天,生产平衡率为85%,设备利用率为74%。最优IMOGWO排产方案如图5所示。
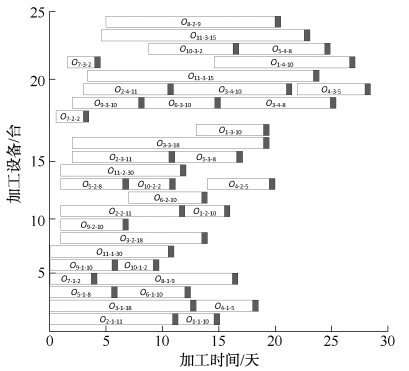
图 5 最优 IMOGWO 排产方案
对比经验排产方案,优化后的排产方案最长完工时间缩短了6天,同时,生产平衡率提高了14%,设备利用率提升了11%。结果表明:优化后的排产方案不仅缩短了生产所需时间,还提升了设备利用率和生产平衡率,从而提高了车间生产效率和产能。
药品作为特殊工业制品,受严格法规监管。制药行业中,中间体库存在时间限制和容量约束,必须在规定时间内完成生产,并控制库存在合理范围内,以避免污染和过期风险。因此,对中间体库存进行分析可以验证排产方案的有效性和优化库存管理。
通过对比两种排产方案的中间体库存仿真模型(图6),发现基于人工经验的排产方案产生的最大库存约为1 800万片,而采用IMOGWO算法得到的最优排产方案,最大库存约为1 450万片,显示出较小的库存压力。与传统人工经验排产方案相比,IMOGWO算法生成的最优排产方案在中间体临时库存方面明显改善。
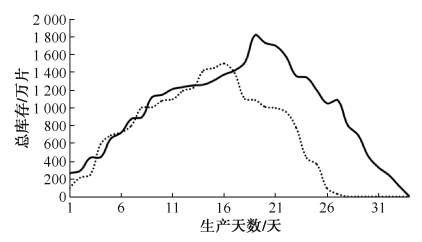
图 6 在制品库存量对比图
3.4.3 算法对比
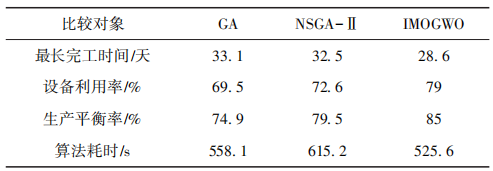
为了验证IMOGWO算法的效果,将其与遗传算法(GA)、非支配排序遗传算法(NSGA-Ⅱ)对3.1节中的药品算例进行优化对比,测试软硬件环境均相同。不同算法对于问题特性和搜索空间的需求存在差异,因此,在选择变异率和交叉率时需要进行权衡。通过平衡全局搜索和局部搜索的考虑,根据具体问题的特点和搜索空间的要求进行参数调整,最佳参数设置需要通过试验和对比来确定。在此次试验中,遗传算法(GA)的交叉率为0.5,变异率为0.4,并采用锦标赛选择算子;而非支配排序遗传算法(NSGA-Ⅱ)的交叉率为0.4,变异率为0.3。3种算法的种群数量均为200,迭代次数为200次,重复运行了20次,并选择各项指标的最优结果进行比较。具体的算法比较结果如表4所示。
表 4 算法指标对比
Part.04结 论
文中针对制药车间的复杂生产工艺、多品种小批量生产效率低及频繁清洗换型等问题,提出了一种综合考虑最小化完工时间、最大化生产平衡率和最大化设备利用率的排产优化模型。通过引入动态加权策略和基于IMOGWO算法的求解方法,获得了显著优越的排产方案。与传统的经验排产方法相比,IMOGWO算法在最长完工时间、生产平衡率和设备利用率方面均得到了显著改善。通过Anylogic软件进行仿真验证,结果显示:IMOGWO算法改善后的排产方案在制品临时库存方面也取得了明显的效果,验证了算法的有效性。然而,实际车间生产中存在许多不确定性因素,如临时插单、供货延迟及设备故障等,需要进一步完善排产算法以应对其复杂性和工艺特征。
参考文献
[1] 安鑫. 免疫遗传算法在中药制药车间调度的研究[D]. 昆明:昆明理工大学, 2011.
[2] 姜天华. 基于灰狼优化算法的低碳车间调度问题[ J].计算机集成制造系统, 2018, 24(10): 2428-2435.
[3] 崔琪, 吴秀丽, 余建军. 变邻域改进遗传算法求解混合流水车间调度问题[J]. 计算机集成制造系统, 2017, 23(9): 1917-1927.
[4] 姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控
邵丽竹
何发
热点文章
-
制药分离技术在生物制药中的应用与探究
2025-12-12
-
中国药典2025年版“药品包装用塑料材料和容器指导原则”的框架体系与核心内容解析
2026-02-04
-
压片制粒生产各过程关键因素之考量
2025-12-22
-
药品共线生产中的清洁验证与风险管控
2025-12-25
-
生物制品分段委托生产情形下的持有人质量管理体系关注点探讨
2025-12-16
-
制药行业未来趋势洞察:数智化、个性化、可持续与全球化重塑产业格局
2025-12-10
-
底喷微丸包衣工艺参数对包衣效果的影响分析
2025-12-04
-
基于CFD仿真技术的灌装机充氮装置设计优化
本文以某制药产线的灌装机设备为研究对象,采用计算流体动力学(CFD)仿真技术对充氮装置的充氮性能进行分析,并结合分析结果对氮幕结构进行了优化设计。随后,针对优化方案进行性能仿真验证,结果显示优化后的顶空残氧量降低至0.252%。为了进一步验证优化方案的实际效果,将优化方案应用于实际产线进行性能测试,测得的顶空残氧量为0.68%,这一结果满足了小于1%的要求,表明其充氮保护性能已达到国际先进水平。
作者:王志刚、刘依宽、刘佳鑫
-
药品密封性检测 :用户需求与优化
-
可控冻融系统在生物原液上的应用
-
人用疫苗生产数字化转型
-
药包材生产质量管理的进阶策略
-
药厂洁净区域风量和压差的控制策略
















评论
加载更多