基于多元动因驱动的中药制药车间动态调度建模与优化

赵培瑞邓超朱波闫文斌梁敏谌敏 2025-07-28

以最小化最大完工时间为优化目标，从原料短缺、临时插单、机器故障等多个动态因素出发构建基于多元动因驱动的中药制药车间动态调度问题(DSP-CMMPW-MDF)模型，并提出一种基于Q-learning的改进人工蜂群(IABC-QL)算法进行求解。

以最小化最大完工时间为优化目标，从原料短缺、临时插单、机器故障等多个动态因素出发构建基于多元动因驱动的中药制药车间动态调度问题(DSP-CMMPW-MDF)模型，并提出一种基于Q-learning的改进人工蜂群(IABC-QL)算法进行求解。在IABC-QL算法中，采用了反向学习策略生成初始种群以确保种群个体的高质量和多样化。为提高算法的深度挖掘能力，设计了融合Q-learning的5种局部搜索操作。在此基础上将上述所提DSP-CMMPW-MDF模型和算法运用于某中药制药颗粒剂生产车间，结果表明，所提模型能够有效提高生产系统在面对不确定性因素时的灵活性和适应性，与现有算法对比结果验证了所提算法的有效性。

Part0节能技术在冷水机组中的应用重要性

中医药产品具有多品种、多规格、多批量的特点，一般按照市场的需求进行拉式生产。传统中药品大都靠人工的方式安排生产，随着信息化、智能化水平的不断提高，智能排产已经开始崭露头角，在高效利用有限资源的情况下可提高生产效率。花植等[1]结合中药生产的特点，将遗传算法应用于中药生产调度，在一定程度上有效解决了中药生产调度问题，并设计出了中药制药系统的原型。罗亚波等[2]针对中药提取车间生产周期长、物料浪费严重，实际生产时生产相关时间和物料损失之间存在着复杂的制约关系，导致调度难度高，排产效率低的问题，以最小化完工时间和物料总损失量为优化目标，提出了一种改进的进化算法。从上述文献可知，现有对中药制药车间调度的研究主要集中于静态环境，通常假设生产要素是确定的。然而，中药制药车间是一个特殊的生产调度环境，制药过程约束多，动态影响因素多，使得实际生产往往与计划之间存在较大差异，造成生产过程不可控。

动态调度能够提高调度方案的准确性和稳定性，是应对生产中不确定性的一种有效方法[3]。NOUIRI等[4]从机器故障的角度研究了基于绿色动态柔性作业车间的动态调度问题，设计了部分重调度策略，构建了混合整数线性规划模型，并采用粒子群优化算法(PSO)进行求解，成功缩短了最小生产周期、减少了能源消耗。PENG等[5]从机器故障导致生产中断的角度研究了炼钢-精炼-连铸工艺中的混合流水车间动态调度问题，考虑连铸阶段的加工时间可控，采用6个现实目标的加权和来衡量进度质量，设计了连铸阶段作业之间的优先约束，并提出了一种改进的人工蜂群(improved artificial bee colony, IABC)算法进行求解。CALDEIRA等[6]从新作业到达的角度研究了柔性作业车间的动态调度问题，构建了一个部分重调度混合整数线性规划模型，设计了一种基于松弛的插入重调度策略，提出了改进的回溯搜索算法进行求解，达到了缩短最小化最大完工时间和减少能源消耗的目标。GAO等[7]从新作业到达的角度研究了柔性作业车间的动态调度问题，考虑了模糊处理时间和新作业插入约束，构建了一个完全重调度混合整数线性规划模型，并提出两阶段人工蜂群算法对模型进行求解，成功求解出了最小化最大模糊完工时间。LYU等[8]从具有替代工艺计划的角度研究了节能柔性作业车间动态调度问题，设计了针对新工作到来和机器故障的重新安排机制，构建了混合整数规划优化模型，并提出了多目标模拟退火算法进行求解，以实现对模型的有效优化。从上述文献可知，现有的动态调度研究大多基于事件驱动的方法，主要针对单一动态因素进行分析，缺乏对多重动态因素相互作用的综合考量和协同优化，这导致在应对复杂多变的生产环境时难以找到最优解，在面对多种不确定性因素时的适应性和鲁棒性不足。

数据驱动技术为复杂多变的动态调度问题提供了有效的解决方案[9-10]。运用数据驱动技术[11-12]能够将多种突发情况综合考虑，构建出涵盖多种实际因素影响的动态调度模型。因此，本文结合数据驱动技术构建了一个在机器故障、紧急插单以及原料未到达等多重动态因素驱动下的中药制药车间动态调度模型，并以最小化最大完工时间为优化目标提出了一种基于Q-learning的改进人工蜂群算法对其进行求解。

Part1问题描述及数学模型

1.1问题描述

中药制药生产具有多品种、多规格、多批量的特点，针对市场需求波动和生产资源动态变化等问题，本文同时考虑临时插单、临时故障和原料缺货未到达三种突发事件对生产线的影响，提出了以最小化最大完工时间为目标的动态调度问题，并将该问题建模为基于多元动因驱动的中药制药车间动态调度问题(dynamic scheduling problem of Chinese materia medica pharmaceutical workshop driven by multiple dynamic factors, DSP-CMMPW-MDF)。

文中涉及符号的说明如表1所示，问题模型如图1所示。

表1 数学模型注释

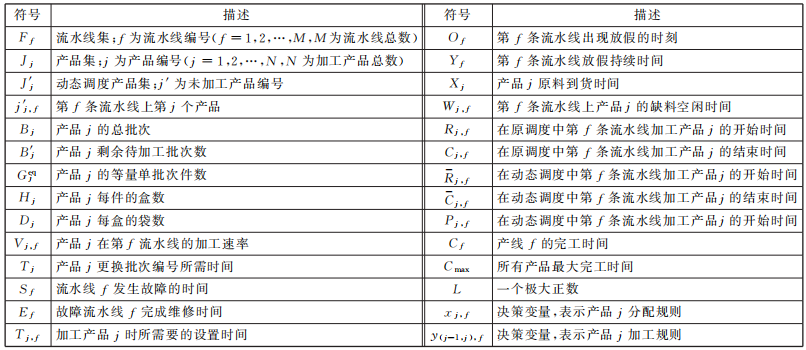
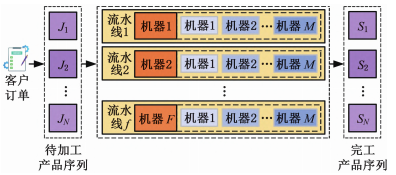
图1 车间示意图

模型描述如下：现存在N个待加工的产品Jj(j=1,2,…,N),需要在M条流水线Ff(f=1,2,…,M)上加工，每个待加工的产品有多条流水线可以选择，其加工顺序按照规定的产品顺序进行，其中产线设置时间与产线上一产品种类、规格有关，产品加工速率已知，且规格不同生产速率不同。在此基础上，考虑上述三种突发事件，在任一时刻，发生临时插单情况下，存在A个插单产品，则未加工产品集为Jj′(j′=1,2,…,N-A),存在B个撤销产品，则未加工产品集为Jj′(j′=1,2,…,N-B);在任一时刻，发生临时故障情况，存在C条故障产线，则可用流水线集为Ff′(f′=1,2,…,M-C)。在原料缺货情况下，产品Jj原料到货时间被推迟，使得产品Jj最早开始时间延迟到Xj。为了更好地描述其数学模型，作如下假设：①所有产品相互独立且在零时刻均可加工，加工产线均可用；②原料到货时间和放假时间提前已知；③假期可以在任一时刻，发生在任一产线上；④当产线出现假期时，生产作业会被延后；⑤产线出现假期时，不存在同一批次被中断的情况；⑥机器故障后可修复，且修复时长已知；⑦产线加工过程不可中断，若该产线发生故障，则该产品被分配到其他产线上加工；⑧临时插单情况默认原料能够满足生产条件，不存在原料未能到达情况；⑨出现突发情况时，同一时刻只会出现一种突发情况。

1.2基于多元动因驱动的动态调度数学模型构建

在DSP-CMMPW-MDF中，初始排产计划是在接收订单后生成的，之后提交给物料部门确认物料是否到位。若物料满足条件，则按计划进行生产；否则，需要根据物料的到货时间重新调整计划。然而，生产过程中可能出现紧急订单、原材料到达时间延迟或设备故障等问题，要求系统具备灵活性和快速反应能力。因此，需要基于多元数据驱动技术设计符合问题特性的动态调度策略，实时调整排产计划，以应对实际生产中的变化。本文以最小化最大完工时间为优化目标，表达式如下：

Cmax=min{max(Cf)} (1)

1.2.1 初始调度模型

产品j只能够在指定流水线f上加工，其约束条件如下：

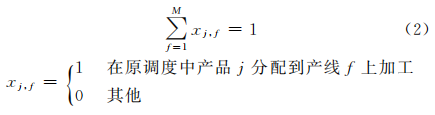
同一条产线在同一时间最多只能加工一个产品，其约束条件如下：

产品j的开始时间应不小于该流水线f的上一个产品j-1的完工时间加上产线设置时间(从上一个工件切换到下一个工件所需要的时间),即

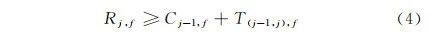
产品开始加工时间一定不小于产品原料到货时间，即

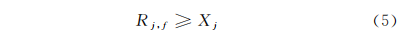
第f条流水线上第j个产品的加工时间为

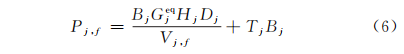
产品j的完工时间应不小于产品j开始加工时间加上产品j所需加工时间,即

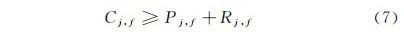
当存在假期情况时,会出现生产被假期中断的情况,因此除式(2)~ 式(7)外补充以下约束条件。

1)处于放假之前的产品j开始时间应不小于该产线f 上一产品j-1完工时间加上产线设置时间,即

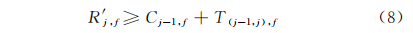
2)产品j在放假时刻已经完成批次的结束时间应不大于放假开始时间,即

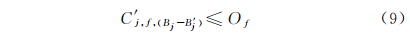
3)产品j剩余批次加工开始时间应不小于放假结束时间(放假开始时间加上流水线j 上放假持续时间),即

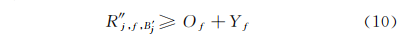
4)产品剩余批次完工时间C″j,f,B'j 应不小于产品剩余批次的开始加工时间 Pj,f,B'j 加上剩余批次所需加工时间Rj,f,B'j ,即

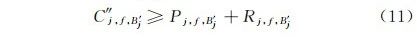
1.2.2 基于多元动因驱动的动态调度模型

本文在初始调度模型的基础上，考虑生产环境中的多种动态因素，并结合多元数据驱动技术，设计了一个能够适应多重动态因素影响的动态调度模型，如图2所示。通过实时数据的驱动，该模型能够确保排产方案的时效性、准确性和高效性，从而最大限度地减少生产中断和延误，提高生产系统的稳健性与响应能力。

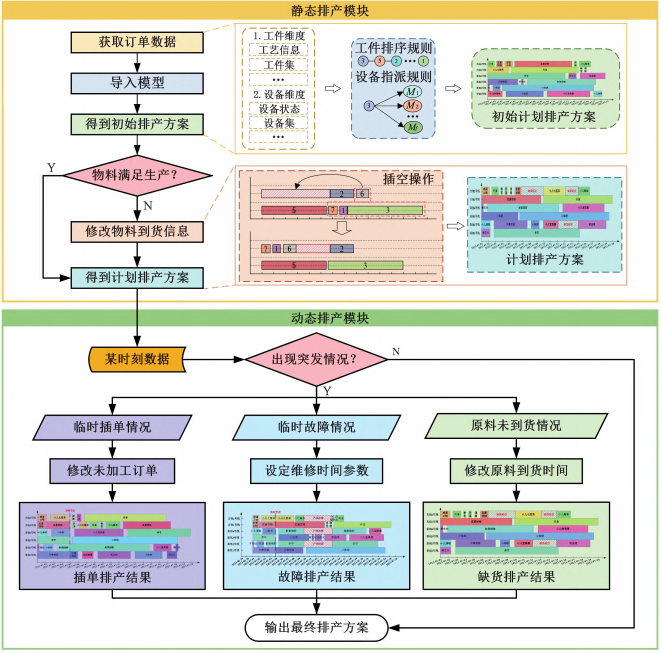
图2 基于多元动因驱动的动态调度模型

1.2.2.1 原材料缺货情况下的动态调度模型

为了应对原料未能及时到达而导致生产延后的特殊情况，设计了一种插空策略，如图3所示。具体实现步骤如下：①识别瓶颈工件，确定哪些工件由于原料未到而导致生产延后；②筛选可插入工件，在同一条产线上查找可以立即加工且不受原料供应影响的工件；③将可插入工件提前插入到瓶颈工件的前面，以确保产线在等待原料的过程中仍然能够持续运作；④根据原料的到达时间和工件的加工情况动态调整工件的排程顺序，确保生产计划的灵活性和高效性。

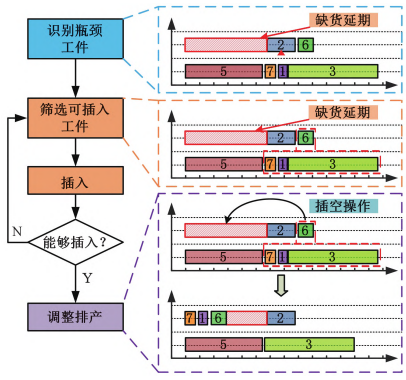
图3 插空策略

这种插空策略不仅可以有效解决因原料延迟导致的生产延后问题，还能显著提高生产线的整体利用率和生产效率。当出现原材料不满足生产时，除式(2)～式(11)外补充以下约束条件。

1)无假期或者假期之前插空产品j的开始加工时间不小于上一产品完工时间与产线设置时间之和，即

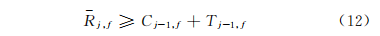
2)假期之后插空产品j的开始加工时间应不小于该产线上一产品j-1的完工时间加上产线设置时间之和与放假结束时间的最大值，即

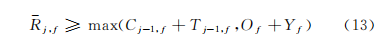
3)插空产品j的完工时间不小于产品所需加工时间与产品开始加工时间之和，即

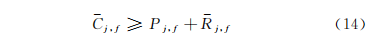
4)未能插空产品j的开始加工时间不小于产线完工时间与产线设置时间之和，即

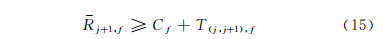
5)未能插空产品j的完工时间不小于产品开始加工时间与产品所需加工时间之和，即

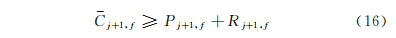
1.2.2.2 临时插单/撤单情况下的动态调度模型

临时插单/撤单是指生产过程已经开始后，由于紧急订单或客户需求的变化，需要将新的生产任务加入到已经排定的生产计划中的情况。以下情况均被视为临时插单/撤单：①原订单中排在后面的产品被前移或者排在前面的产品被后移；②原订单中同批次产品被要求分段生产；③原订单中产品全部被撤销或者部分被撤销；④新增订单。当出现临时撤单情况时，将剩余产品顺次提前；

当出现临时插单情况时除式(2)～式(16)外，另补充以下约束。

1)产品的开始加工时间应不小于该产线上一产品的完工时间加上产线设置时间，即

2)产品的结束时间应不小于产品开始加工时间加上产品所需加工时间，即

3)在动态调度中，当存在假期情况时，产品在放假时刻已经完成批次的结束时间应不大于放假开始时间，即

4)产品中剩余批次继续加工的开始时间应不小于放假结束时间，即

5)产品中剩余批次完工时间应不小于产品中剩下的批次继续加工的开始时间加上剩下的批次继续加工的所需时间，即

1.2.2.3 机器故障情况下的动态调度模型

在生产过程中,当产线发生故障时,采用完全重调度策略 (CR)。相关操作需在式 (2)~ 式(16)之外补充相应约束条件。

1)产品开始加工时间应不小于该产线上一产品与故障修复时间中的最大值加工设置时间:

2)产品的完工时间不小于该产品批次所需加工时间加上产品开始加工时间:

3)在动态调度中,当存在假期情况时,产品在假期之前的批次结束时间应不大于放假开始时间与维修时间的最小值,即

4)产品剩余批次继续加工的开始时间应不小于放假结束时间与维修时间的最大值,即

5)产品剩余批次完工时间应不小于产品中剩下的批次继续加工的开始时间加上剩下的批次继续加工的所需时间,即

Part2基于Q-learning的改进人工蜂群算法求解多元动因驱动下的中药制药车间调度问题

2.1编码和解码

1)编码。本文采用基于操作的排列编码，即获取所有工件序号进行随机排列，从而形成个体，个体长度等于待加工的产品数，工件在个体中的位置代表工件的加工顺序。例如，某中药制药车间有10个待加工的产品，根据优先级依次对产品进行编号P={5,2,7,1,3,6,4,10,9,8},则P表示先加工工件5,然后依次对工件2,7,1,3,6,4,10,9,8进行加工。

2)解码。在解码过程中，依据最早完工时间(earliest completion time, ECT)规则对个体进行解码。首先针对每条产线确定其最早可能的完工时间，然后计算流水线的完工时间，并将下一个工件指派到最早完工的流水线。

2.2初始化种群

为了兼顾初始种群的质量和多样性，采用反向学习策略(opposition-based learning, OBL)[13]来初始化种群。反向学习策略(图4)同时考虑个体及其反向个体，可以提高种群覆盖搜索空间的能力，从而提高优化算法的效率。初始化过程如下：

1)设定种群个体数为N。

2)随机生成N个个体，记为种群P1。然后，对随机生成的N个个体进行反向学习，生成对应的反向种群P2。反向个体的生成设工件编号的最小数为1,最大数为n,当前工件编号为Ji,则Ji的反向学习

3)将随机生成的种群P1和通过反向学习生成的种群P2合并，得到合并种群P。

4)对合并后的种群个体进行适应度排序，选出适应度最好的N个个体作为初始种群。

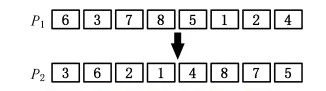
图4 染色体的反向学习策略

2.3雇佣蜂搜索阶段

在雇佣蜂搜索阶段，本文采用两种邻域操作，即交叉和变异。具体操作如图5所示。该阶段操作过程如下：引入控制参数α(用来控制迭代次数)。种群中的个体都要进行α次邻域操作，通过随机概率选择邻域操作，如果随机变量为1则进行NS1操作；如果随机变量为2则进行NS2操作。其中邻域操作NS1指在工件序列中，随机选取两个具有不同位置的工件号进行交换，得到新的序列。邻域操作NS2指将工件序列中的一个工件从当前位置移动到序列中的另一个位置，同时顺序调整其他工件位置。若邻域解X*l与原始解Xl相比有所改进，则更新解；若邻域解比原始解差，则保留原始解舍弃邻域解，并记录更新失败次数LXl。雇佣蜂搜索阶段详细过程(算法1)如下：

图5 雇佣蜂阶段邻域操作

2.4跟随蜂搜索阶段

跟随蜂阶段，本文采用二元锦标赛选择策略选择种群中的个体。在该策略中，随机选择两个个体进行竞争，并从中选出获胜者。获胜个体采用与雇佣蜂阶段相同的方法生成新的邻域解。若邻域解优于种群中的最差个体Xworst并且优于当前个体，则最差解被替换。若邻域解优于当前最佳解，则更新当前最佳解。跟随蜂搜索阶段详细过程(算法2)如下：

2.5侦察蜂搜索阶段

侦察蜂阶段，本文采用增强策略来生成新个体。该策略对指定迭代限制内未更新的个体进行随机搜索，以避免穷举搜索，从而提高算法效率。该阶段操作过程如下：引入控制参数L(用来记录个体更新失败次数)和φ(用来表示丢弃个体的迭代次数)来防止算法陷入局部最优。如果个体的迭代更新失败次数大于L,则丢弃该个体。被丢弃的个体经过φ次随机插入操作，产生φ个候选个体。之后选择候选个体中的最优个体作为新个体。如果选择的个体优于当前最佳解，则更新当前最佳解。如果比当前最佳解差，则该个体被舍弃。侦察蜂搜索阶段详细过程(算法3)如下：

2.6基于Q-learning的局部搜索

经典的元启发式算法容易陷入局部最优且收敛效率低，因此，本文根据问题的特点，针对种群中的优质解设计了五种局部搜索策略LS1～LS2以提高收敛速度并快速找到高质量的解：①LS1,在工件序列中，随机选取两个具有不同位置的工件进行交换；②LS2,在工件序列中，随机选取两个具有不同位置的工件进行两次交换；③LS3,在工件序列中，随机移除一些具有不同位置的工件并将其作为整体插入到原序列中，保留完工时间最小的新序列；④LS4,在工件序列中，随机移除一些具有不同位置的工件，按照移除顺序一个接一个插入到原序列中，保留完工时间最小的新序列；⑤LS5,在工件序列中，随机移除一些具有不同位置的工件，将其按原相对位置逆序作为整体插入到原序列中，保留完工时间最小的新序列。

为了更好地解释上述邻域操作，以个体P={5,2,7,1,3,6,4,10,9,8}为例。算子对工件的交换、插入位置是随机选择的，并用下划线标明，如表2所示。本文利用Q-learning算法来动态选择局部搜索阶段的搜索策略，Q值的更新公式如下：

其中，Q(st,at)为对当前状态st执行动作at获得的Q值，A为学习率，R为奖励值，γ为折扣率，maxQ(st+1,at+1)表示在状态st+1下选择动作at+1时通过轮盘赌策略获得的最高预期Q值。

表2 局部操作示例

R 奖励值的公式如下:

式中:C'为新值;C 为旧值。在迭代开始时,Q 表(一个X ×Y 矩阵)中的Q 值是相同的。每当算法执行某个局部搜索策略时,Q 表中相应的Q 值就会改变。每次迭代后,Q表都会进行更新。Q 值较大,Q-learning就有较大概率指导算法选择对应局部搜索操作。针对优质解的局部搜索策略详细过程(算法4)如下:

2.7算法整体流程

算法整体流程如图6所示。具体流程如下：

1)初始化参数和种群。设置种群规模(ps),最大运行时间(T),个体更新失败最大迭代次数(L),雇佣蜂阶段迭代次数(α)以及侦察蜂阶段个体最大迭代次数(φ),学习率(A),折扣率(γ),Q表。使用2.2节中的方法生成初始种群。

2)雇佣蜂阶段。对种群中每一个个体，随机进行交叉、变异操作。重复这个过程直到种群个体全部被执行了α次。

图6 算法流程图

3)跟随蜂阶段。采用二元锦标赛策略选择个体。使用与雇佣蜂阶段相同方法为选定个体生成新个体。如果搜索后得到的解优于群体中的最差个体并且优于当前个体，则邻域解取代最差解。如果邻域解优于当前最佳解，则更新当前最佳解。

4)侦察蜂阶段。遍历种群中的个体，如果个体在连续迭代中超过L次未被更新，则丢弃该个体，对丢弃个体进行φ次变异操作，生成φ个邻域解，选取最佳邻域解个体放回种群中。如果无个体超过L,则执行下一步。

5)局部搜索阶段。对种群进行排序，选取前10%的个体进行基于Q-learning的局部搜索，通过Q表选取动作更新个体。

6)若达到终止条件，则输出最佳解；否则，转步骤2)。

Part3仿真实验结果与分析

3.1关键参数设置

本节实验中，使用L1-L2-N表示问题规模，其中L1表示条包线数量，L2表示方包线数量，N表示工件数量。所有算法程序均在MATLAB R2022a下编程实现，实验设备为CPU:12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz, RAM 16.0 GB。

首先对算法的4个关键参数进行基于实验设计方法的实验分析，从而确定算法全局参数的最优组合，这4个参数是种群规模(ps),连续更新失败的最大次数(L),雇佣蜂阶段邻域解数量(α)以及侦察蜂阶段生成的邻域解的数量(φ)。实验开始时，为每个参数选择了几个典型值，如表3所示。基于四参数四水平因子，选择正交矩阵L16,生成16种不同的参数组合。对于每个参数组合，从基准库中选择中等规模(4-2-60)进行正交试验，每组参数组合均分别进行10次独立实验，实验最大运行时间T由问题规模决定，即T=(L1+L2)N,单位为s。最后将得到的相对改进百分比(RPI)值的平均值(ARPI)作为响应结果，如表4所示。相对改进百分比为

式中：c为同一规模相同实例的目标值；cmin为同一规模相同实例的最小目标值。

表3 4个参数取值

表4 4个不同参数组合的 ARPI值

ARPI指标(ωARPI)反映了算法在多次实验中所达到的最优解的平均水平,值越小表示所需加工时间越短,意味着算法具有更好的优化能力。

然后对基于 Q-learning的局部搜索阶段的两个关键参数(A 和γ)进行基于实验设计方法的实验分析,从而确定算法局部参数的最优组合。实验采用上述正交试验所得到的全局参数,之后为A 和γ 选择几个典型值,如表5所示。基于两参数四水平因子,选择正交矩阵 L16,生成16种不同的参数组合。对于每个参数组合,从基准库中选择中等规模(4-2-60)进行正交试验,每组参数组合均分别进行10次独立实验,最大时间限制为(4×2×60)s。最后将得到的 RPI的平均值(ωARPI)作为响应结果,结果如表6所示。

表5 两个参数取值

表6 两个不同参数组合的 ARPI值

图7、图8显示了因子水平趋势,ωAPRI 值越小,性能越好。可以明显看出,当种群规模ps =40时,与其他规模相比ωARPI 值最小;雇佣蜂阶段邻域解数量α=20的时候效果最佳;个体连续更新失败的最大次数越多,反而效果越差,因此选取L=5;对于侦察蜂阶段,邻域解数量φ为10、15的性能优于φ 为5、20的性能,证明了侦察蜂阶段的有效性。针对局部搜索部分,当学习率 A =0.6,折扣率γ =0.2时,ωARPI 值最小,验证了局部搜索的有效性。根据上述分析,最终设置的参数为:种群规模ps=40,雇佣蜂阶段邻域解数量α=20,个体连续更新失败的最大次数L=5,侦察蜂阶段生成的邻域解的数量φ=10,学习率A=0.6,折扣率γ =0.2。

图7 算法全局参数水平趋势

图8 算法局部搜索参数水平趋势

3.2基于Q-learning的局部搜索有效性

为了验证基于Q-learning的局部搜索有效性，将基于Q-learning的改进人工蜂群算法IABC-QL与未使用局部搜索的算法IABC进行对比，其中参数规模完全相同，以相同运行时间作为终止条件。为此，设置实验规模为25组实验，最大运行时间为T。分别独立运行10次进行实验。从表7中的结果可以看出，在25个测试算例中，带局部搜索的改进人工蜂群算法在独立运行10次后，不同规模下其平均最优值始终小于或等于未使用局部搜索情况下的平均最优值。这一结果充分证明了局部搜索在优化过程中的有效性。

表7 局部搜索有效性算法比较结果

3.3基于多元动因驱动的某中药制药车间动态调度模型运用实例

以某中药制药企业某月的实际订单为例(扫描本文首页OSID码获取具体信息),在综合考虑多重实际因素的基础上，将订单导入模型进行优化排产。图9展示了正常状态下无干扰的计划排产方案甘特图。由图可见，该企业中药制药车间共有6条产线，其中4条为条包类型产线，2条为方包类型产线。此外，不同品种规模(简称品规)之间存在大小不一的间隔，这些间隔表示生产下一个品规时产线所需的设置时间(即清洗换模时间，扫描OSID码获取具体信息)。图10展示了假期影响下的计划排产方案甘特图。由图可见，由于生产不能在假期进行，因此一些品规如丹溪玉屏风、小儿七星茶和风寒感冒等被拆分成了两部分，分别在假期前和假期后进行加工。

图9 无假期影响计划排产甘特图

图10 受假期影响计划排产甘特图

在得到的计划排产方案基础上模拟计划阶段原料未到货情况。图11展示了原料缺货情况下且无假期影响的计划排产方案甘特图。由图可见，该月订单中存在原料不满足生产条件的品规：小儿七星茶、小儿解表、千紫红和板蓝根。其中，小儿七星茶最早的加工时间为7月10日，小儿解表为7月15日，板蓝根为7月15日，千紫红无准确到达日期故删除该品规，整个订单共用时22天。采用插空策略后的计划排产方案总用时缩短至19天。

图11 原料缺货情况下的甘特图

图12分别展示了原料缺货情况下且受假期影响的计划排产方案甘特图以及采用插空策略后的甘特图。由图可见，不使用插空策略的情况下，总用时为23天；使用插空策略后，总用时缩短至21天。上述数据均验证了插空策略的有效性。

在得到的计划排产方案基础上，开始模拟加工过程中临时插单突发情况。图13展示了在无原料缺货且无假期影响情况下的动态调度排产甘特图。由图可见，实时节点之前表示已经加工完成的品规。其中，玄麦甘菊、风寒感冒和小儿七星茶未被完全加工完成，被拆分成了两部分。此外，止泻保童和风热感冒为临时插单且需紧急交付的品规。

图12 受假期影响的原料未到货甘特图

在得到的计划排产方案基础上，开始模拟加工过程中产线临时故障突发情况。图14展示了在无原料缺货且无假期影响情况下的动态调度排产甘特图。由图可见，条包2号线、条包4号线、方包2号线在7月5日发生故障，预计7月10日完成维修恢复生产。

图13 临时插单甘特图

在得到的计划排产方案基础上，开始模拟加工过程中多种突发情况并存情况。图15展示了在临时原料缺货且受产线故障及临时插单影响情况下的动态调度排产甘特图。由图可见，条包1号线、条包3号线和方包5号线在7月5日发生故障，并于7月8日完成维修恢复生产。止泻保童和风热感冒为临时插单且需紧急交付的品规。此外，丹溪玉屏风、小儿解表和板蓝根的最早加工时间为7月15日。

3.4仿真实验与结果分析

为验证本文所提算法的有效性，将用于求解并行机混合流水车间调度问题的改进粒子群算法(IPSO)[14]、并行批处理机柔性作业车间调度问题的增强多种群遗传算法(EMPGA)[15]、改进灰狼算法(SS-GWO)[16]以及求解排列流水车间调度问题的混合灰狼算法(HGWO)[17]与本文所提算法进行比较。参数设置均选用文献中的最优参数，基于Q-leaning的改进人工蜂群算法参数设置同3.1节。为验证算法有效性，选取了某中药制药企业的实际订单量和生产规模，生成相应的测试数据集。设置实验规模为25组实验，最大运行时间为T,分别独立运行10次进行实验。表8以平均最优值为评价指标对实验结果进行统计。由表可见，随着问题规模的增大，IABC-QL的求解有效性变得明显。IABC-QL在25个实验中得到的值均比其他四种算法得到的值小，由此表明IABC-QL能有效求解此类问题。

图14 临时故障甘特图

图15 多种突发情况并存的排产甘特图

Part4结语

本文针对多重实际因素影响下的中药制药车间调度问题，以最小化最大完工时间为目标，提出了一种基于Q-learning的改进人工蜂群算法(IABC-QL)进行求解。仿真实验结果表明，本文提出的算法在求解效率和效果方面均优于其他算法，验证了其有效性和优越性。在未来的研究中，将进一步考虑以下方面。

1)扩展现有模型，以涵盖中药制药过程中多阶段的调度问题，提供更全面的调度解决方案。

2)引入更多实际生产中的复杂约束和优化目标，考虑更多实际生产中广泛存在的复杂约束和优化目标，使问题模型更贴合生产实际的需求，进一步提升模型的适用性和实用性。

3)结合其他算法与机器学习技术，探讨运用其他先进算法来解决该问题，并将优化算法与机器学习技术相结合，以进一步提高算法的性能和效率。

参考文献

[1] 花植,郭剑毅,王海雄,等.基于遗传算法的中药生产调度原型系统研究及应用[J].云南大学学报(自然科学版),2009,31(增刊

2):200-204.HUAZhi,GUOJianyi,WANG Haixiong,etal.ResearchandApplicationofaPrototypeSystemforTCMProductionSchedulingBasedonGeneticAlgorithm[J].Journalof Yunnan University(NaturalSciences),2009,31(S2):200-204.

[2] 罗亚波,王洲旭.基于改进进化算法的中药提取车间批调度问题研究[J].工业工程与管理,2024,29

(4):89-100.LUO Yabo,WANG Zhouxu.Research on BatchSchedulingProbleminTCM Extraction WorkshopBasedonImprovedEvolutionaryAlgorithm[J].IndustrialEngineering and Management,2024,29(4):89-100.

[3]GHALEB M,TAGHIPOORS,ZOLFABARINIAH.Real-timeIntegratedProduction-schedulingandMaintenance-planninginaFlexibleJobShop withMachineDeteriorationandCondition-Based Maintenance.[J].Journal of Manufacturing Systems,2021,61:423-449.

[4]NOUIRIM,BEKRARA,TRENTEAUXD.TowardsEnergyEfficientSchedulingandRescheduling forDynamicFlexibleJobShopProblem.[J].IFACPapersOnline,2018,51(11):1275-1280.

[5] PENG Kunkun,PAN Quanke,GAO Liang,etal.AnImproved ArtificialBeeColony Algorithm for Real-worldHybridFlowshopReschedulinginSteelmaking-refining-continuous Casting Process [J].Computers & IndustrialEngineering,2018,122:235-250.

[6] CALDEIRA R H, GNANAVELBABU A,VAIDYANATHAN T.An EffectiveBacktracking Search Algorithm for Multi-objectiveFlexibleJob ShopSchedulingConsideringNewJobArrivalsand

EnergyConsumption.[J].Computers & Industrial Engineering,2020,149:106863.

[7]GAOK,SUGANTHANPN,PANQ,etal.ArtificialBeeColonyAlgorithmforSchedulingandReschedulingFuzzyFlexibleJobShopProblem with NewJobInsertion.[J].Knowledge-basedSystems,2016,109:1-16.

[8] LYU Yan,LICongbo,TANGYing,etal.Toward Energy-efficientReschedulingDecisionMechanisms

forFlexibleJobShopwithDynamicEventsandAlternativeProcessPlans[J].IEEETransactionson AutomationScienceandEngineering,2021,19(4):3259-3275.

[9] ZHANG Q, GROSSMANN I E, SUNDARAMOORTHY A,etal.Data-drivenConstructionof ConvexRegionSurrogate Models[J].Optimization andEngineering,2016,17:289-332.

[10] QIAOFei,LIUJuan,MA Yumin.IndustrialBigdata-driven and CPS-based Adaptive Production SchedulingforSmart Manufacturing[J].Interna

tionalJournalofProduction Research,2021,59(23):7139-7159.

[11]MOURTZISD,VLACHOUE.ACloud-basedCyber-physicalSystemforAdaptiveShop-floorSchedulingandCondition-based Maintenance[J].Journalof ManufacturingSystems,2018,47:179-198.

[12]LIYuxin,GUWenbin,WANGXianliang,etal.Data-drivenSchedulingforSmartShopFloorvia

ReinforcementLearningwithModelBasedClusteringAlgorithm[C]∥2021IEEE4thAdvancedInformationManagement,Communicates,Electronicand AutomationControlConference(IMCEC).Chongqing:IEEE,2021,4:1310-1314.

[13] TIZHOOSH H R.Opposition-based Learning:a NewSchemeforMachineIntelligence[C]∥InternationalConferenceonComputationalIntelligence forModelling,ControlandAutomationandInternationalConferenceonIntelligent Agents, Web Technologies and Internet Commerce(CIMCAIAWTIC'06).Vienna:IEEE,2005,1:695-701

[14] 顾文斌,李育鑫,钱煜晖,等.基于激素调节机制IPSO 算法的相同并行机混合流水车间调度问题[J].计算机集成制造系统,2021,27(10):2858-2871.GUWenbin,LIYuxin,QIANYuhui,etal.SchedulingProblem ofIdenticalParallel MachineHybridFlowShopBasedontheIPSOAlgorithmwithHormoneRegulation Mechanism[J].ComputerIntegratedManufacturingSystems,2021,27(10):2858-2871.

[15]XUELirui,ZHAOShinan,MAHMOUDIA,etal.FlexibleJobshopSchedulingProblemwithParallelBatchMachinesBasedonanEnhancedMultiPopulationGeneticAlgorithm[J].Complex&IntelligentSystems,2024,10(3):4083-4101.

[16]ZHOUKai,TANChuanhe,ZHAOYi,etal.Researchon Solving FlexibleJob Shop Scheduling ProblemBasedonImprovedGWO Algorithm SSGWO[J].NeuralProcessingLetters,2024,56:26.

[17] CHEN Shuilin,ZHENG Jianguo.Hybrid Grey Wolf Optimizer for Solving Permutation Flow ShopScheduling Problem [J].Concurrency and Computation:Practiceand Experience,2024,36(5):e7942.

责任编辑：邵丽竹

审　　核：何发

基于多元动因驱动的中药制药车间动态调度建模与优化

评论

热点文章