EMA和FDA指南中提到了溶出曲线比较的一般建议。
然而,除了计算相似因子f2之外,EMA和FDA都没有提供用于比较溶出曲线的明确说明。
根据EMA和FDA比较溶出曲线的策略,本文概述了合适的统计方法(基于bootstrap的f2因子CI推导、参考样品和供试样品之间差异的CI推导、马氏距离、模型相关方法和最大偏差方法)、其方法和局限性。
然而将统计方法用于上述方法可能会遇到困难,特别是当与用于数据评估的稳健和简单技术的实践要求相结合时。因此,选择bootstrap导出f2的CI或参考样品和测试样品之间差异的CI导出作为选择的方法。
介绍
溶出度研究确定活性药物成分(API)在规定的时间间隔内在规定的溶出介质中从测试剂型中的体外释放。溶出度测试得出的详细API溶出曲线代表了最基本的剂型特征之一。
溶出度测试通常用于在药物开发和质量控制过程中提供关键的体外药物释放信息。它也应用于新药和仿制药的开发。在开始生物等效性研究之前,它在比较不同药品的溶出曲线方面起着至关重要的作用。
溶出度测试是评估药品质量和稳定性的重要工具。对API释放进行合格评估的首要先决条件是选择具有独特特征的适当溶出方法,该方法可以清楚地检测单个剂型API释放的主要差异,理想情况下是在模拟人体或动物体内真实药物吸收的条件下。FDA在其网站上公布了在美国注册的单个API的溶出方法列表。
实验溶出数据可用于预测药物从剂型中的释放速率和机制。将API释放量表示为时间函数的各种数学模型通常用于处理溶出数据。由于获得的溶出曲线的非线性(零级动力学除外),应首选使用非线性回归分析来评估原始测量数据。测量数据到线性形式的相关性变换(例如,幂或对数变换)导致偏差大小的变化,并且偏差的平方和不会被所得函数最小化。
溶出数据分析的一个重要领域是评估溶出曲线之间的相似性。已经开发了几种方法来比较溶出曲线。为此,Moore和Flanner提出的f2方法因其简单性而成为欧洲药品管理局(EMA)和FDA的首选指标。f2相似性因子用于评估溶出曲线的整体相似性,并且不需要关于数据生成过程的任何假设。
如果批次之间存在显著差异,则在比较两种药物溶出曲线时使用f2点估计值是不合适的。为了避免这个问题,EMA和FDA指南允许使用其他依赖于模型或独立于模型的方法进行溶出曲线比较。
如上所述,模型相关方法将由某个数学函数表示的模型拟合到数据上。相似性区域是基于来自测试单元的拟合模型的估计参数的变化而导出的。与模型无关的方法根据多元统计距离确定相似性极限。本文旨在详细概述FDA和EMA提到的用于比较溶出曲线的方法,包括其程序和局限性。
EMA和FDA指南中的溶出曲线比较
EMA和FDA指南允许使用不同的方法进行溶出曲线比较。一般建议使用至少12个单位(例如,一个单位代表例如片剂)的测试(T)和参比(R)产品来确定溶出曲线的相似性。仅当使用足够数量的采样时间点对溶出曲线进行了令人满意的表征时,才能认为溶出曲线相似性试验有效。
当超过85%的药物在15分钟内溶解(这意味着(R)和(T)样品的药物释放的平均百分比)时,溶出曲线可以被认为是相似的,而无需进一步的数学评估。
如果不满足前面的要求,相似性因子f2由于其简单性,是EMA和FDA选择的指标。当f2统计量不合适时,EMA指南建议“(...)可以使用模型相关方法或模型独立方法(...)来比较相似性”,并且这些替代方法必须“(...)统计上有效且合理”。
除了f2统计量之外,已经开发和研究了几种与模型无关的方法,例如Rescigno指数、比率检验方法、基于方差分析(ANOVA)模型的方法或基于曲线下面积计算溶出效率。
不幸运的是,EMA和FDA指南并不清楚上述模型无关方法示例的可接受性。EMA指南仅说明了如果使用某种替代方法,通常应满足哪种条件。该条件是“(...)相似性可接受限度应预先定义并证明其合理性,且差异不大于10%”和“(...)供试品和参比品的溶出度变异性也应相似,但供试品的较低变异性可能是可接受的”。
另一方面,FDA指南更具体地涉及基于模型相关方法的相似性评估,即基于拟合数学函数的曲线与溶出曲线的比较。以下部分描述了比较溶出曲线的基本方法、统计方法概述以及EMA和FDA指南背景下的建议(见图1)。
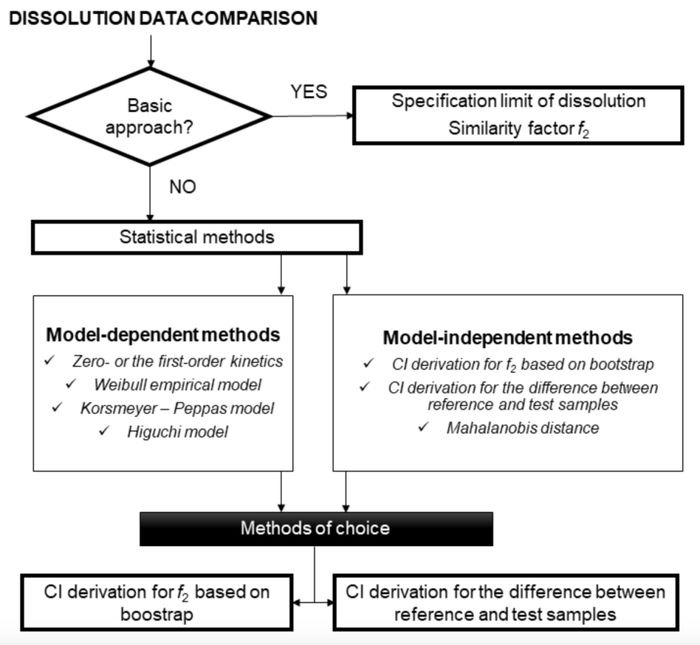
图1 EMA和FDA指南溶出度数据比较策略的示意图
2.1相似因子f2
一种简单的与模型无关的方法使用相似因子f2来比较溶出曲线。相似因子f2是(T)和(R)曲线之间的平方差和的对数平方根倒数变换,并且它表示“平均”溶出曲线之间溶出百分比(%)的相似性的测量,即,
其中n是时间点的数量,Rt和Tt分别是在t时间点从(R)和(t)产品中释放的药物的平均百分比,1≤t≤n。等式(1)中的对数是十进制的,即以10为基数。
相似因子达到0到100的值。值100表示相同的溶出曲线。与值0相差可忽略的负值指示轮廓之间的最大百分比相异,即在每个非零时间点,第一产品为0%,第二产品为100%。
根据EMA和FDA指南,
50-100范围内的f2值表明溶出曲线的相似性。
FDA指南中提供了更精确的陈述,即f2的值必须严格大于50才能具有相似性。基于f2,如果在每个时间点释放的药物的平均百分比在(T)和(R)产物之间相差至少10%,则确实认为溶出曲线不相似。在这种情况下,f2总是小于50。
相似因子f2不能用于任意溶出数据。根据EMA和FDA指南,必须满足以下先决条件:
(2)两种产品至少考虑三个时间点(不包括时间零点);
(5)任何产品的平均百分比值高于85%的不超过一个;
(7)(非零)时间点应小于20%,在以下时间点应小于10%。
如果不满足f2计算的至少一个先决条件,例如某些时间点的CV值超过最大允许值,则必须使用其他方法来评价溶出曲线的相似性。在这方面,EMA指南更喜欢用自举法构建f2的置信区间(CI)(见第2.2节)。
相反,FDA指南更喜欢在原始溶出度数据(见第2.4节)或拟合原始溶出度数据的回归模型估计参数(见第2.5节)上使用一些多元统计距离(其中马氏距离是最常见的例子)。
应该提到的是,不满足使用f2的至少一个先决条件似乎不是唯一的问题。即使(R)和(T)样品在某个时间点(或多个时间点)溶解的药物平均百分比的差异大于10%,也可以用f2得出溶出曲线相似性。它与相似性验收限度不一致,相似性验收限度应“(...)不大于10%的差异”,如EMA指南中所述,指的是单个时间点的10%差异。
因此,评估(T)和(R)产品之间溶出曲线相似性的替代统计方法应与f2一起使用,以符合最大10%差异标准。该标准可以是每个时间点(T)和(R)产品之间差异的CI估计值,其中所有CI应完全在相似性可接受限度内(参见第2.3节)。
根据FDA指南,也可以使用差异因子f1进行溶出曲线比较。差异因子是(T)产品和(R)产品之间的差异的绝对值相对于从(R)产品中释放的药物的平均百分比之和。这种评估溶出曲线相似性的方法基于与使用相似性因子时相同的原理。
在0-15范围内的f1的计算值表明(T)和(R)产物之间的溶出曲线相似性。值0对应于相同的溶出曲线(包括两种产品在每个时间点具有相同的零平均释放药物百分比的特殊情况)。
有趣的是,如果(T)产物在每个非零时间点接近最大溶出度(~100%),并且同时(R)产物在每个非零时间点接近最小溶出度(~0%),则f1可以具有理论上无界的上限。文献中给出了差异因子计算的细节。
差异因子f1和相似因子f2代表用于比较体外溶出曲线的简单且经常使用的工具。这种方法的使用不需要统计学领域的深厚知识,也不需要特殊的软件。
如果满足上述先决条件,这是首选方法。
如果不满足f2计算的至少一个先决条件(例如,某些时间点的CV值高于最大可接受值),EMA和FDA指南建议使用一些替代方法来评价溶出曲线的相似性。EMA指南倾向于基于bootstrap方法构建f2的CI(第2.2节)。
FDA指南更喜欢使用一些多元统计距离,例如马氏距离(参见第2.4节))或基于溶出度数据回归分析的回归参数的溶出度曲线比较(参见第2.5节)。
CI推导如前所述,如果单独的f2统计量不合适,EMA推荐用于推导f2 CI的Bootstrap方法。如Islam和Begum中所述,bootstrap“(...)是统计推断的计算密集型方法(...)基于通过从具有替换的数据中重新采样获得的统计的采样分布”,这使得能够导出“(...)感兴趣的统计的精确采样分布”。感兴趣的统计量是f2,并且基于其采样分布的知识,可以获得f2的自举CI。对于溶出数据,包括两种产品的12个曲线(这是使用f 2的许多曲线的最低要求),优选使用所谓的非参数自举来构建f2的CI。
Mendyk等人创建了统计开源软件“PHEQ_Bootstrap 1.2版”来评估溶出曲线的相似性,其原理基于EMA法规下的bootstrap方法。
(1)通过从原始溶出度数据重新采样来生成n个bootstrap样品(例如5000个);
(2)为n个自举样本中的每一个计算f2,即,存在n个新的F2值;
关于点(1),自举样本中的测试(参考)简档是从原始数据中的测试(参考)简档重新采样的。关于第(3)点,Islam和Begum得出结论,用于计算导致bootstrap CI下限和上限的百分位数的偏差校正和加速方法表现最佳。当bootstrap CI的下限完全高于50时,得出基于F2的bootstrap CI的溶出曲线相似性[23]。它还满足EMA指南中更精确的要求,即“(...)f 2值在50和100之间(...)”对于相似性意味着f 2必须大于50。
Islam和Begum提到,应该使用f2的双侧90%引导CI,优选双侧95%引导CI。bootstrap方法允许研究人员对高度可变的数据集进行比较,并由于限制了异常值的影响而获得可靠的结果。
如上所述,在不满足f2计算的先决条件并且不适合单独使用F2统计量的情况下,EMA支持这种方法。与传统方法(f2因子计算)相比,基于bootstrap的f2 CI推导需要更深入的统计学知识,但使用特殊软件(例如,Mendyk创建的统计开源软件)可以促进计算。
基于EMA指南中的声明“(...)相似性可以使用(...)在不同时间点的溶解百分比(...)”,溶出曲线统计比较的另一种简单方法是分别计算(T)和(R)样品之间相对于每个时间点释放药物的平均百分比的差异的CI。考虑到EMA指南[12]中的声明,即差异应“(...)不大于10%(...)”,如果每个时间点(T)和(R)样品之间估计差异的CI完全在区间(10%,+10%)内,则溶出曲线可被认为是相似的。CI的下限和上限可以根据以下表达式来估计:
其中Rt和Tt分别是(R)和(T)样品在t时间点释放的药物的平均百分比;Qp是相关概率分布的p分位数,其中从区间(0,1)中选择数字p以获得CI的目标置信水平;nT,T和nR,T分别表示(R)和(T)样本的测量次数,在t-时间点;st2是在t-时间点使用分别来自(R)和(T)样本的方差sR、t2和sT、t2的加权平均值估计总体方差的合并方差。因此,方差的合并估计由等式表示:
原则上,等式(2)基于重写双样本t检验的检验统计量。在这种情况下,如果满足以下假设,(2)中的分位数Qp是具有nT,t+nR,t-2个自由度的t分布的p分位数(在t-时间点对(t)和(R)乘积减去2的观测值的数量):
通常,考虑差异的双侧95%CI,对应于Qp的p=0.975。
例如,双样品t检验的缺点可以从忽略不同时间点之间相同曲线的测量溶出度的依赖性中看出。由多变量双样本Hotelling T2检验的检验统计量的分布产生的分位数可用于克服这一限制。在文献中,已经详细描述了使用T2统计的溶出曲线比较。
相似性因子F2的潜在替代方案可以是马氏距离(MD),这是多变量统计距离的最常见示例。
一般来说,马氏距离是点和分布之间的距离(而不是两个不同点之间的距离)。如果该点位于分布的平均值,则MD等于零,如果该点远离平均值,则MD增加。
使用MD评估(R)和(T)产品之间溶出曲线的相似性基于给定时间(R)和(T)产品的药物释放量平均值向量的比较。(R)和(T)产物溶出数据的MD根据:
其中T和R分别是(T)和(R)产品在给定时间释放的药物的平均百分比值的向量;(T-R)T是差向量(T-R)的转置;S1是经验协方差矩阵S的(现有)逆矩阵。应当注意,在实际计算中,经验协方差矩阵S基于(R)乘积的协方差矩阵与(T)乘积的协方差矩阵的合并。
此外,假设存在n个测量溶出度的时间点。在这种情况下,平均值和平均值之间的差的向量具有n个分量,并且经验协方差矩阵是n × n矩阵。经验协方差矩阵解释了不同时间点之间溶出度的依赖性。向量与等式(4)中协方差矩阵的逆相乘得到MD作为具有非负值的标量。
对于MD的计算,可以使用已经实现等式(4)的PC软件(例如,R统计软件,PythonTM)。如果协方差矩阵S是单位矩阵,那么它的逆S-1也是单位矩阵,并且MD减小到欧几里得距离。对于MD的估计值,可以计算90%或95%CI。基于MD值评估轮廓相似性的关键步骤是确定等效裕度θ(相似性阈值)。为了计算θ,差向量(T−R)和(T−R)T应该是具有10的向量,以符合EMA指南中的条件,即差应该“(...)。
在每个时间点,(T)和(R)产品之间的差异不大于10%”。方程(4)中的逆矩阵S-1由从测量的溶出曲线导出的合并协方差矩阵S计算。如果MD的CI上限低于当量界θ的值,则可以认为溶出曲线相似。
换句话说,如果MD的CI完全在区间【0,θ)内,则得出相似性,其中区间的下限使用等式(4)中定义的MD具有最小值零的事实。应该提到的是,一些作者同意这样的观点,即与基于等式(4)的裕度相比,等效裕度应该是预定义的固定数,除了选择的差异向量(T−R)和(T−R)T之外,等效裕度还受经验协方差矩阵S的倒数的影响。
Hoffelder【30】详细描述了当前基于MD的多元等效程序。Hoffelder在溶出曲线比较的背景下不仅讨论了欧几里德和MD的使用。此外,他还提到了当前文献中MD的关键时刻。
EMA于2018年发布了一份关于MD评估药物溶出曲线可比性的充分性的文件。在本文件中,EMA倾向于使用bootstrap方法推导f2的CI,不推荐使用MD进行溶出曲线比较。上述不确定性可能会影响EMA的建议,主要是因为没有给出等效限度,并且溶出数据集之间曲线相似性的定义可能不同。
最大偏差方法在f2度量不合适的情况下,也可以使用模型相关方法评估溶出曲线的相似性。该方法基于将回归模型拟合到溶出曲线(最常用的模型见表1)、模型参数的估计以及用于相似性评估的产品之间模型参数的比较。Muselík等人最近发表的文章详细总结了溶出曲线回归分析的基本步骤。
对于基于模型相关方法的溶出曲线比较,FDA指南建议将不超过三个参数的模型拟合到每个单独的曲线,对估计的参数应用一些多元统计距离(MSD),得出MSD的90%CI或90%置信区域(CR),如果90%CI或90%CR完全位于相似性区域内,则得出溶出曲线相似性的结论。EMA指南没有具体说明相似性评估,除了应用于威布尔模型估计参数的MSD的可能可接受性。
Mt为时间t释放的药物量,k0为零级释放速率常数,参数b表示时间t=0时溶出介质中的非零溶出药物量Mt,M∞为无限时间内剂型可释放的最大药物量,k1为一级释放速率常数,kw为威布尔模型常数,参数β(威布尔模型)表征指数曲线的形状,kKP是Korsmeyer-Peppas模型的常数,kH是Higuchi模型的常数,M’t是在时间t的剂型中的药物量,kHC是Hixson-Crowell模型的常数,kHP是Hopfenberg模型的常数。
然而,根据FDA指南中的声明,尚不清楚如何推导估计模型参数的相似性区域。此外,还有一个问题是为什么FDA指南建议仅使用模型参数的点估计进行基于MSD的相似性评估。尽管如此,没有考虑点估计的标准误差。
关于模型参数的相似区域的选择,解决方案可以是将(R)和(T)产品的所有溶解剖面拟合到同一回归模型中(例如,使用OriginPro®9、GraphPad Prism®7)。相同的回归模型显然能够在产品之间比较相应的回归参数。回归模型应在同一时间点对(T)和(R)产物的所有溶出曲线进行最佳拟合,以便在拟合过程中尽可能多地使用信息。该模型还应以这样的形式考虑,即可以表示(T)和(R)乘积之间的差异。
然后,基于(R)和(T)轮廓的所选模型的函数值之间的差异,制定产品之间模型参数的估计值差异的相似性标准。套用EMA指南,对于特定时间范围内的每个时间点t,(t)和(R)曲线之间释放药物百分比的绝对值差异不应大于10%,即t(t)-R(t)≤10。以这种方式,估计参数之间的可接受差异被定义为对每个时间点处的函数值之间的差异的限制。
关于包括标准误差(1-α),上述(T)和(R)乘积的估计参数之间的差异的100%CI可以根据。
其中tv,1-α是t分布的(1-α)分位数,其中v=nT,t+nR,T-2个自由度(反映观测值总数减去2),α来自区间(0,1)。选择α的值以获得CI所需的置信水平(通常1−α=0.975,以获得方程(5)中差异的双侧95%CI)。如果基于等式(5)的(R)和(T)样品之间差异的CI完全在范围内,最多反映溶出曲线之间10%的差异,则可以认为(R)和(T)产物的溶出曲线相似。
可以给出没有截距项的零级动力学模型的例子,即t(t)=kT t和R(t)=kR t(其中kT和kR分别是(t)和(R)产物的释放常数)。参数之间差异的标准是kt-kr≤10/t。这形成了相似性区域[-10/t,+10/t],差异kt-kr的CI必须完全位于其中。相似性区域的下限和上限取决于来自特定时间范围的时间t,并且时间单位与用于拟合回归模型的时间单位相同。
如果存在截距项(“突发效应”),则同时为截距项和斜率项创建CR(通常为90%或95%)。因此,对于来自同时CR的两个参数值的所有组合,必须满足相似性条件。
例如,考虑具有截距项的零级动力学模型,即t(t)=k0T+kT t和R(t)=k0R+kR t,相似性的条件是(k0t-k0r)+(kt-kr)t≤10,时间t选自某个时间范围。对于来自导出的同时CR的k0T、kT、k0R和kR的所有组合,必须满足该条件。然而,考虑截距项会导致相同的回归模型分别拟合到(T)和(R)剖面的情况。描述了比较两个简单线性回归模型之间的参数和推导同时CR的方法。
应该注意的是,等式(5)最适合于零阶、KorsmeyerPeppas或Higuchi模型。在这些模型中,对于(T)和(R)产物的所有溶出曲线同时使用相同的模型,可以容易地导出参数之间的绝对差异,以得出关于相似性的结论。
如果所用模型的估计参数在非线性函数的自变量中,则模型参数的相似性准则的表达变得更加复杂。例如,在T(t)=M∞(1-exp(-kT t))和R(t)=M∞(1-exp(-kR t))的一级动力学模型的情况下,必须使用近似方法来导出差异kt-kr的相似性准则。
假设两种产品的最大释放量M∞相同,则可能的选择是使用导致M∞(kt-kr)t≤10的一阶泰勒多项式和相似性区域(-10/(M∞t),+10/(M∞t))。该区域不仅取决于时间t,还取决于最大释放M∞。
在这种情况下,差异kt-kr的相应CI可以基于等式(5)使用从分别拟合到(T)产物的所有溶出曲线和分别拟合到(R)产物的所有溶出曲线的模型获得的估计值及其标准误差来推导。缺点是差异kt-kr的相似区域没有被精确地表示。
此外,非线性模型的同时CR的推导更加复杂。如果参数kT和kR来自单独的(但相同的)非线性回归模型,则该难度甚至更高。
为了避免在“逐个案例”的基础上对相似性区域和CR进行复杂的推导,提出了一种替代方法。这种方法被称为最大偏差(MAXDEV)方法,它基于对差异的评估:
式中,t(t,β t)和R(t,β r)分别为拟合(t)和(R)乘积样本的参数回归曲线;β t、β r为相应回归参数的向量;t表示距区间M的时间。零假设(H0,等式(7))与备选假设(H1,等式(8))的关系公式化为:
其中∆是预先指定的正数。在EMA指南中关于在每个时间点最大容忍10%差异的声明的背景下,选择是=10。H0的公式是,对于(T)和(R)样品的所选模型,溶出曲线不相似,因为最大绝对差异超过∈。为了更好地近似d∞在H0下的分布,基于参数自举估计d∞的CI,并对估计的模型参数进行限制。如果d∞的CI完全位于区间(0,∈)中,其中区间的下限来自d∞被定义为非负值的事实,则得出溶出曲线之间的相似性。
MAXDEV方法的优点是同时考虑了测量溶出度之间的可变性、时间依赖性和溶出曲线的形状。当拟合的回归模型对于(T)曲线和(R)曲线不同时,该方法似乎有能力克服这个问题,尽管作者仅在为两种产品选择的相同模型上证明了MAXDEV方法的性能。由于自举是参数的,因此溶出曲线的自举样本基于从一些参数分布的自举。
具体地,MAXDEV方法从具有零均值和协方差结构的正态分布自举残差,该结构是从所得残差估计的根据应用于原始溶出数据的拟合模型。基于bootstrap样本,估计原始拟合模型的模型参数并计算d∞值。
最后,使用百分位数法寻找d∞估计分布的合适分位数,以获得bootstrap CId∞的请求置信水平。Moellenhoff等人。在三个真实数据集和一个人工数据集上测试了MAXDEV方法的性能。
基于人工数据集,与构建F 2 90%CI的自举方法相比,1型错误概率(T1EP)控制在5%(相似性标准:90%CI的下限必须高于50),其中T1EP被夸大(~55%)。关于T1EP的陈述是在d∞的H0中对=10做出的,正如作者可能知道的那样。它符合(T)和(R)产物之间溶出度差异的条件“(...)不应大于10%”[12]。作者认为,T1EP的差异可能是由d∞需要在每个时间点的差异“一致”小于10%才能得出相似性的结论,而f 2即使在某个时间点的差异至少为10%也可以评估相似性(另见第2.1节中的简要提及)。对于d∞≤8的值,MAXDEV方法的统计功效高于80%,然后下降(例如,d∞=9的功效约为30%)。Bootstrap F2的功率通常更高,但代价是膨胀的T1EP,正如作者提到的,这种膨胀“(...)从监管的角度来看是不可接受的”。
使用依赖于模型的方法需要(i)适用于描述不同类型溶出曲线的数学模型的知识,(ii)非线性回归分析原理的知识和(iii)合适的软件。这种方法的关键点是模型参数相似性准则的表达,特别是如果估计参数在非线性函数的自变量中。MAXDEV方法提供了避免相似性区域和CR的复杂推导的可能性。此外,这种方法的优点是它克服了当(T)和(R)剖面的拟合回归模型不同时的问题。
释放曲线评价通常涉及溶出曲线的比较(例如,仿制药与品牌药的比较、药品的稳定性试验)。文献中描述了几种适用于比较溶出曲线的不同方法。
本文旨在概述监管机构支持的方法。根据FDA和EMA指南,比较溶出曲线的主要方法是相似因子f2。在两种产品在15分钟内释放药物的平均百分比高于85%的情况下,不需要使用相似性因子f2,并且自动认为曲线相似,而无需任何进一步的数学评估。
在其他情况下,考虑相似性因子f2(如果满足其所有先决条件)或一些替代统计方法(如果违反了使用F2的至少一个先决条件)。在比较溶出曲线的背景下,EMA和FDA描述的一些方法(例如,马氏距离、模型依赖性方法)存在一些局限性(例如,指南未提及相似性标准)。
另一方面,用于推导f2 CI的bootstrap是一种可接受的方法,在体外溶出曲线的统计比较中具有明确设定的标准。一种可接受的方法也可以是基于CI的计算及其与预定义限度的比较,比较(T)和(R)样品之间关于不同时间点溶解百分比的差异。
基于上面的讨论,基于bootstrap的f 2的CI推导和参考样品和测试样品之间的差异的CI推导可以被认为是选择的方法。这两种方法满足监管机构的要求,克服了统计评估中的困难,对于实践中的常规使用来说是稳健和简单的,并且允许评估不同类型的溶出数据。























评论
加载更多